Şimdiye kadar, ikinci dereceden denklemleri kareyi tamamlama, karenin farkı ve mükemmel kare üç terim formülü gibi yöntemlerle nasıl çözeceğinizi biliyorsunuz.
Bu makalede, aşağıdakileri nasıl yapacağımızı öğreneceğiz ikinci dereceden denklemleri iki yöntem kullanarak çözebilir, yani kuadratik formül ve grafiksel yöntem. Bu konuya girmeden önce, ikinci dereceden denklemin ne olduğunu hatırlayalım.
İkinci Dereceden Denklem Nedir?
Matematikte ikinci dereceden bir denklem, standart formu ax olan ikinci dereceden bir polinom olarak tanımlanır2 + bx + c = 0, burada a, b ve c sayısal katsayılardır ve a ≠ 0’dır.
İkinci derece terimi, denklemdeki en az bir terimin ikinin kuvvetine yükseltildiği anlamına gelir. İkinci dereceden bir denklemde x değişkeni, çözümünü bulmamız gereken bilinmeyen bir değerdir.
İkinci dereceden denklemlere örnekler: 6x² + 11x – 35 = 0, 2x² – 4x – 2 = 0, 2x² – 64 = 0, x² – 16 = 0, x² – 7x = 0, 2x² + 8x = 0 vb. Bu örneklerden, bazı ikinci dereceden denklemlerde “c” ve “bx” terimlerinin eksik olduğunu görebilirsiniz.
İkinci dereceden formül nasıl kullanılır?
Diyelim ki ax2 + bx + c = 0 standart ikinci dereceden denklemimizdir. Aşağıda gösterildiği gibi kareyi tamamlayarak ikinci dereceden formülü türetebiliriz.
c terimini denklemin sağ tarafında izole edin
balta2 + bx = -c
Her terimi a ile bölün.
x2 + bx/a = -c/a
Tam kare olarak ifade edin
x 2 + bx/a + (b/2a)2 = – c/a + (b/2a)2
(x + b/2a) 2 = (-4ac+b2)/4a2
(x + b/2a) = ±√ (-4ac + b2)/2a
x = – b/2a ±√ (b2 – 4ac)/2a
x = [- b ±√ (b2 – 4ac)]/2a………. (Bu kuadratik formüldür)
İkinci dereceden formülde artı (+) ve eksi (-) işaretlerinin bulunması, aşağıdaki gibi iki çözüm olduğunu gösterir:
x1 = (-b + √b2 – 4ac)/2a
VE,
x2 = (-b – √b2 – 4ac)/2a
Yukarıdaki iki x değeri ikinci dereceden denklemin kökleri olarak bilinir. İkinci dereceden bir denklemin kökleri diskriminantın doğasına bağlıdır. Diskriminant, b şeklinde ikinci dereceden formülün bir parçasıdır 2 – 4 ac. İkinci dereceden bir denklemin diskriminantının iki farklı reel kökü vardır.
Diskriminant değeri sıfır olduğunda, denklemin yalnızca bir kökü veya çözümü olacaktır. Diskriminant negatifse, ikinci dereceden denklemin gerçek kökü yoktur.
İkinci Dereceden Denklemler Nasıl Çözülür?
İkinci dereceden formülü kullanarak birkaç problem örneği çözelim.
Örnek 1
x’in köklerini bulmak için ikinci dereceden formülü kullanın2-5x+6 = 0.
Çözüm
Denklemin ax genel formu ile karşılaştırılması2 + bx + c = 0 verir,
a = 1, b = -5 ve c = 6
b2 – 4ac = (-5)2 – 4×1×6 = 1
Değerleri ikinci dereceden formülde yerine koyun
x1 = (-b + √b2-4ac)/2a
⇒ (5 + 1)/2
= 3
x2 = (-b – √b2-4ac)/2a
⇒ (5 – 1)/2
= 2
Örnek 2
Aşağıdaki ikinci dereceden denklemi ikinci dereceden formülünü kullanarak çözünüz:
3x2 + 6x + 2 = 0
Çözüm
Problemi ax ikinci dereceden denkleminin genel formu ile karşılaştırma2 + bx + c = 0 verir,
a = 3, b = 6 ve c = 2
x = [- b ± √ (b2– 4ac)]/2a
⇒ [- 6 ± √ (62 – 4* 3* 2)]/2*3
⇒ [- 6 ± √ (36- 24)]/6
⇒ [- 6 ± √ (12)]/6
x1 = (-6 + 2√3)/6
⇒ -(2/3) √3
x2 = (-6- 2√3)/6
⇒ -(4/3) √3
Örnek 3
5x çözün2 + 6x + 1 = 0
Çözüm
İkinci dereceden denklem ile karşılaştırdığımızda, şunu elde ederiz,
a = 5, b = 6, c = 1
Şimdi ikinci dereceden formülü uygulayın:
x = -b ± √ (b2 – 4ac)2a
a, b ve c değerlerini yerine koyun
⇒ x = -6 ± √ (62 – 4×5×1)2×5
⇒ x = -6 ± √ (36 – 20)10
⇒ x = -6 ± √ (16)10
⇒ x = -6 ± 410
⇒ x = – 0.2, -1
Örnek 4
5x çözün2 + 2x + 1 = 0
Çözüm
Katsayılar şunlardır;
a = 5, b = 2, c = 1
Bu durumda, diskriminant negatiftir:
b2 – 4ac = 22 – 4×5×1
= -16
Şimdi ikinci dereceden formülü uygulayın;
x = (-2 ± √ -16)/10
⇒√ (-16) = 4
Burada i hayali sayıdır √-1
⇒x = (-2 ± 4i)/10
Bu nedenle, x = -0,2 ± 0,4i
Örnek 5
x’i çözün2 – 4x + 6.25 = 0
Çözüm
İkinci dereceden bir denklemin standart formuna göre ax2 + bx + c = 0 olduğunu gözlemleyebiliriz;
a = 1, b = -4, c = 6,25
Ayırıcıları belirleyin.
b2 – 4ac = (-4)2 – 4 × 1 × 6.25
= -9 ………………. (negatif diskriminant)
⇒ x = -(-4) ± √ (-9)/2
⇒ √ (-9) = 3i; burada i hayali sayıdır √-1
⇒ x = (4 ± 3i)/2
Dolayısıyla, x = 2 ± 1,5i
İkinci Dereceden Bir Denklemin Grafiği Nasıl Çizilir?
İkinci dereceden bir denklemin grafiğini çizmek için izlenmesi gereken adımlar şunlardır:
- İkinci dereceden bir denklem verildiğinde, denklemi y veya f(x)’e eşitleyerek yeniden yazın
- Eğriyi çizmek için rastgele x ve y değerleri seçin
- Şimdi fonksiyonun grafiğini çizin.
- Eğrinin x eksenini kestiği veya x eksenine değdiği kökleri okuyun.
İkinci dereceden denklemleri grafikle çözme
Grafik, ikinci dereceden denklemleri çözmenin bir başka yöntemidir. Denklemin çözümü, grafiğin x-kesişimleri okunarak elde edilir.
İkinci dereceden denklemleri grafiksel yöntemle çözerken üç olasılık vardır:
- Grafiğin x-kesimi 1 ise bir denklemin bir kökü veya çözümü vardır.
- İki köklü bir denklemin 2 x-kesişimi vardır
- Eğer x – kesişimleri yoksa, o zaman bir denklemin gerçek çözümleri yoktur.
Şimdi birkaç ikinci dereceden denklem örneğinin grafiğini çizelim. Bu örneklerde grafiklerimizi grafik yazılımı kullanarak çizdik ancak bu dersi çok iyi anlayabilmeniz için grafiklerinizi elle çizin.
Örnek 1
x denklemini çözün2 Grafiksel yöntemle + x – 3 = 0
Çözüm
Keyfi değerlerimiz aşağıdaki tabloda gösterilmektedir:
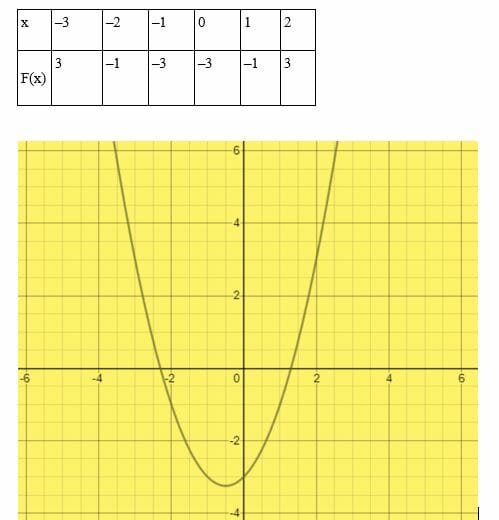
X kesişimleri şunlardır x = 1.3 ve x = -2.3. Dolayısıyla, ikinci dereceden denklemin kökleri x = 1.3 ve x = -2.3’tür.
Örnek 2
6x – 9 – x denklemini çözün2 = 0.
Çözüm
Rastgele x değerleri seçin.
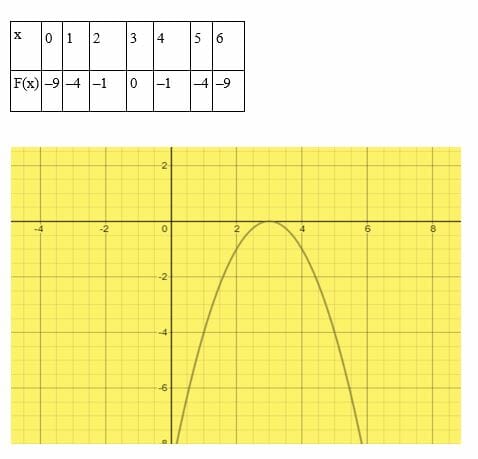
Eğri x eksenine x = 3 noktasında temas etmektedir. Bu nedenle, 6x – 9 – x2 = 0’ın bir çözümü vardır (x = 3).
Örnek 3
x denklemini çözün2 + 4x + 8 = 0’ı grafiksel yöntemle bulur.
Çözüm
Rastgele x değerleri seçin.
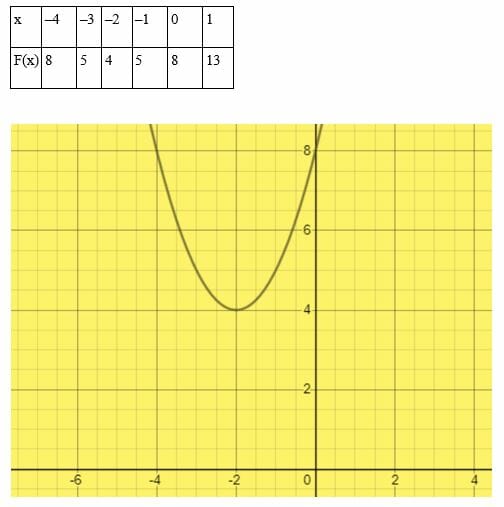
Bu örnekte, eğri x eksenine dokunmamakta veya x eksenini geçmemektedir. Bu nedenle, ikinci dereceden denklem x2 + 4x + 8 = 0’ın herhangi bir reel kökü yoktur.
