Önce doğrusal eşitsizlik sistemlerini çözmeeşitsizliğin ne anlama geldiğine bakalım. Eşitsizlik kelimesi, kenarların birbirine eşit olmadığı matematiksel bir ifade anlamına gelir.
Temel olarak, eşitsizlik denklemlerini temsil etmek için kullanılan beş eşitsizlik sembolü vardır.
Bunlar küçüktür (<), büyüktür (>), küçük veya eşittir (≤), büyük veya eşittir (≥) ve eşit değildir sembolüdür (≠). Eşitsizlikler, sayıları karşılaştırmak ve belirli bir değişkenin koşullarını karşılayan değer aralığını veya aralıklarını belirlemek için kullanılır.
Doğrusal Eşitsizlikler Sistemi Nedir?
Bir doğrusal eşitsizlikler sistemi, aynı değişkenleri içeren bir dizi doğrusal eşitsizlik denklemidir.
Doğrusal denklem sistemlerini çözmenin çeşitli yöntemleri doğrusal eşitsizlikler sistemine dönüşür. Bununla birlikte, bir doğrusal eşitsizlikler sistemi doğrusal denklemlerden biraz farklıdır çünkü eşitsizlik işaretleri yerine koyma veya eleme yöntemiyle çözmemizi engeller. Doğrusal eşitsizlik sistemlerini çözmek için belki de en iyi yöntem eşitsizliklerin grafiğini çizmektir.
Doğrusal Eşitsizlik Sistemleri Nasıl Çözülür?
Daha önce, tek bir doğrusal eşitsizliğin grafiğini çizerek nasıl çözüleceğini öğrenmiştiniz. Bu makalede, aynı anda iki veya daha fazla doğrusal eşitsizliğin grafiğini çizerek bir doğrusal eşitsizlik sistemi için nasıl çözüm bulacağımızı öğreneceğiz.
Bir doğrusal eşitsizlik sisteminin çözümü, sistemdeki tüm doğrusal eşitsizliklerin grafiklerinin üst üste geldiği bölgedir.
Bir eşitsizlik sistemini çözmek için, aşağıdaki adımları izleyerek sistemdeki her bir doğrusal eşitsizliği aynı x-y ekseni üzerinde grafikleyin:
- Her bir doğrusal eşitsizlikte y değişkenini izole edin.
- Sırasıyla > ve ≥ sembolleri için kesikli ve düz çizgiler kullanarak sınır çizgisinin üzerindeki alanı çizin ve gölgelendirin.
- Benzer şekilde, < ve ≤ sembolleri için sırasıyla kesikli ve düz çizgiler kullanarak sınır çizgisinin altındaki alanı çizin ve gölgelendirin.
- Tüm denklemlerin çakıştığı veya kesiştiği bölgeyi gölgelendirin. Kesişme bölgesi yoksa, eşitsizlikler sisteminin çözümü olmadığı sonucuna varırız.
Bu adımları anlamak için birkaç örnek üzerinden gidelim.
Örnek 1
Aşağıdaki doğrusal eşitsizlikler sisteminin grafiğini çizin:
y ≤ x – 1 ve y < -2x + 1
Çözüm
İlk eşitsizlik y ≤ x – 1’in grafiğini çizin.
- “Daha az veya eşit” sembolü nedeniyle, düz bir kenarlık çizeceğiz ve gölgelendirmeyi çizginin altında yapacağız.
- Ayrıca, aynı x-y ekseni üzerinde ikinci y < -2x + 1 eşitsizliğinin grafiğini çizin.
- Bu durumda, less than sembolü nedeniyle sınır çizgimiz kesikli veya noktalı olacaktır. Sınır çizgisinin altındaki alanı gölgelendirin.
Dolayısıyla, bu eşitsizlikler sisteminin çözümü aşağıda gösterildiği gibi sonsuza kadar aşağıya doğru uzanan koyu gölgeli bölgedir.
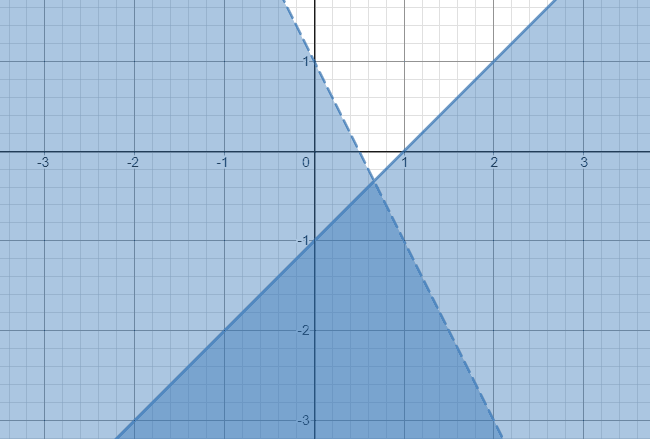
Örnek 2
Aşağıdaki eşitsizlikler sistemini çözünüz:
x – 5y ≥ 6
3x + 2y > 1
Çözüm
- İlk olarak, her eşitsizlikte sol taraftaki y değişkenini izole edin.
x – 5y ≥ 6 için;
=> x ≥ 6 + 5y
=> 5y ≤ x – 6
=> y ≤ 0,2x – 1.2
Ve 3x + 2y > 1 için;
=> 2y > 1 – 3x
=> y > 0,5 – 1,5x
- y ≤ 2 grafiğini çizeceğizx– 1.2 ve y > 0.5 – 1.5x sırasıyla düz bir çizgi ve kesik bir çizgi kullanarak.
Eşitsizlik sisteminin çözümü, iki ayrı çözüm bölgesinin örtüştüğü daha koyu gölgeli alandır.
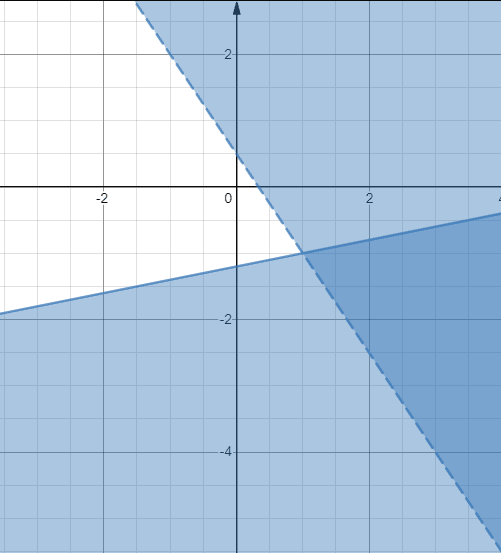
Örnek 3
Aşağıdaki doğrusal eşitsizlikler sisteminin grafiğini çizin.
y ≤ (1/2) x + 1,
y ≥ 2x – 2,
y ≥ -(1/2) x – 3.
Çözüm
Bu eşitsizlikler sistemi, hepsi bir “eşittir” sembolüyle birbirine bağlanan üç denkleme sahiptir. Bu bize tüm sınır çizgilerinin katı olacağını söyler. Üç eşitsizliğin grafiği aşağıda gösterilmiştir.
Üç denklemin gölgeli bölgesi tam orta kısımda çakışmaktadır. Bu nedenle, sistemin çözümleri grafikte gösterildiği gibi sınırlı bölge içinde yer almaktadır.

Örnek 4
Aşağıdaki doğrusal eşitsizlikler sisteminin grafiğini çizin:
x + 2y < 2, y > -1,
x ≥ -3.
Çözüm
Elde etmek için ilk eşitsizlikteki y değişkenini izole edin;
y < – x/2 +1 y > -1 ve x ≥ -3 eşitsizliklerinin sırasıyla yatay ve dikey sınır çizgilerine sahip olacağına dikkat etmelisiniz. Üç eşitsizliğin grafiğini aşağıda gösterildiği gibi çizelim.
İki noktalı doğru parçası ve bir düz doğru parçasının çevrelediği koyu gölgeli bölge üç eşitsizliği vermektedir.
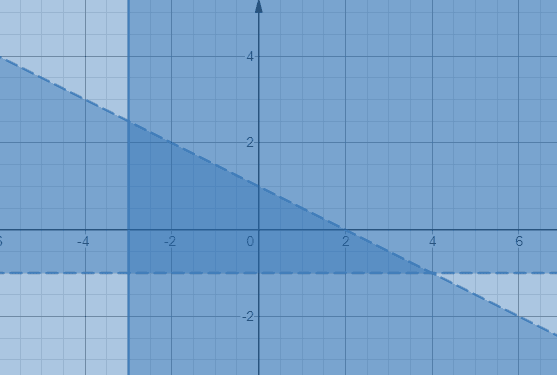
Örnek 5
Aşağıdaki doğrusal eşitsizlikler sistemini çözünüz:
-2x -y < -1
4x + 2y ≤-6
Çözüm
Her eşitsizlikte y değişkenini izole edin.
-2x -y < -1 => y > -2x + 1
4x + 2y ≤ -6 => y ≤ -2x -3
Devam edelim ve y > -2x + 1 ve y ≤ -2x -3 grafiklerini çizelim:
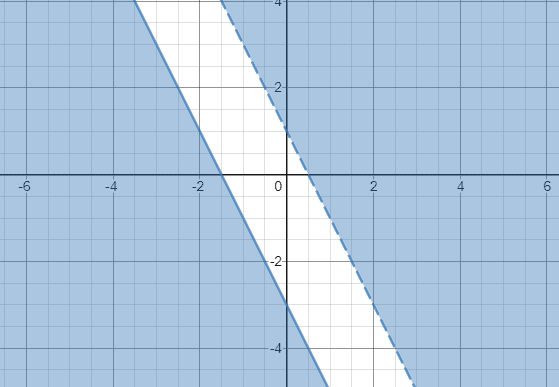
İki eşitsizliğin gölgeli alanları örtüşmediğinden, eşitsizlikler sisteminin çözümü olmadığı sonucuna varabiliriz.
