Doğrusal eşitsizlikler, < (daha az), > (daha büyük), ≤ (daha az veya eşit), ≥ (daha büyük veya eşit) ve ≠ (eşit değil) gibi eşitsizlik sembolleri kullanılarak iki değerin karşılaştırıldığı sayısal veya cebirsel ifadelerdir
Örneğin, 10 < 11, 20 > 17 sayısal eşitsizliklere örnek iken, x > y, y < 19 – x, x ≥ z > 11 vb. cebirsel eşitsizliklere örnektir. Cebirsel eşitsizlikler bazen gerçek eşitsizlikler olarak da adlandırılır.
‘<‘ ve ‘>’ eşitsizlik sembolleri katı eşitsizlikleri ifade etmek için kullanılırken, ‘≤’ ve ‘≥’ sembolleri gevşek eşitsizlikleri temsil eder.
Doğrusal Eşitsizliklerin Grafiği Nasıl Çizilir?
A doğrusal eşitsizlik doğrusal bir denklemle aynıdır, sadece eşitsizlik işareti eşittir işaretinin yerine geçer. Doğrusal denklemlerin grafiğini çizmek için kullanılan aynı adımlar ve kavramlar doğrusal eşitsizliklerin grafiğini çizmek için de uygulanır.
Sadece iki denklem arasındaki fark doğrusal bir denklemin bir doğru grafiği vermesidir. Buna karşılık, doğrusal bir eşitsizlik, eşitsizliği karşılayan koordinat düzleminin alanını gösterir.
Doğrusal bir eşitsizlik grafiği, koordinat düzlemini iki bölgeye ayırmak için genellikle bir sınır çizgisi kullanır. Bölgenin bir kısmı eşitsizliğin tüm çözümlerinden oluşur. Sınır çizgisi, ‘>’ ve ‘<‘yi temsil eden kesikli bir çizgi ve ‘≥’ ve ‘≤’yi temsil eden düz bir çizgi ile çizilir.
Aşağıda bir eşitsizliğin grafiğini çizmek için gerekli adımlar verilmiştir:
- Bir eşitsizlik denklemi verildiğinde, y’yi formülün öznesi yapın. Örneğin, y > x + 2
- Eşitsizlik işaretini eşittir işaretiyle değiştirin ve y ya da x için rastgele değerler seçin.
- Bu keyfi x ve y değerleri için bir çizgi grafiği çizin.
- Eşitsizlik sembolü ≤ veya ≥ ise düz bir çizgi ve < veya > için kesikli bir çizgi çizmeyi unutmayın.
- Eşitsizlik sırasıyla > veya ≥ ve < veya ≤ ise çizginin üstünde ve altında gölgelendirme yapın.
Doğrusal Eşitsizlikler Grafikle Nasıl Çözülür?
Doğrusal eşitsizlikleri grafikle çözmek gerçekten basittir. Eşitsizlikleri çizmek için yukarıdaki adımları izleyin. Çizildikten sonra, gölgeli alan o eşitsizliğin çözümüdür. Birden fazla eşitsizlik varsa, ortak gölgeli alan eşitsizliklerin bir çözümüdür.
Bu kavramı aşağıdaki örnekler yardımıyla anlayalım.
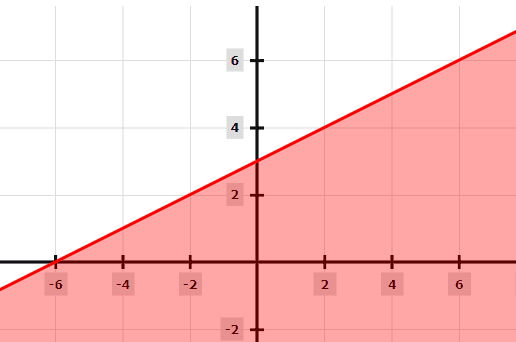
Örnek 1
2y – x ≤ 6
Çözüm
Bu eşitsizliğin grafiğini çizmek için, y’yi formülün öznesi yaparak başlayın.
Her iki tarafa x eklendiğinde elde edilir;
2y ≤ x + 6
Her iki tarafı da 2’ye bölün;
y ≤ x/2 + 3
Şimdi y = x/2 + 3 denklemini ≤ işareti nedeniyle düz bir çizgi olarak çizin. ≤ işareti nedeniyle çizginin altındaki gölge.
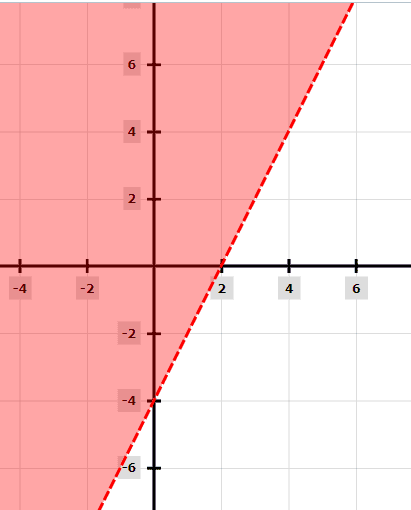
Örnek 2
y/2 + 2 > x
Çözüm
y’yi formülün öznesi haline getirin.
Her iki tarafı da 2 ile çıkarın;
y/2 > x – 2
Kesri ortadan kaldırmak için her iki tarafı da 2 ile çarpın:
y > 2x – 4
Şimdi, > işareti nedeniyle, y = 2x – 4 için kesikli bir çizgi çizin.
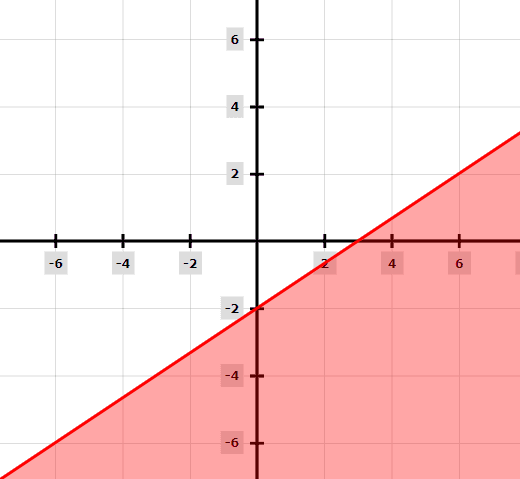
Örnek 3
Aşağıdaki eşitsizliği grafik çizerek çözün: 2x – 3y ≥ 6
Çözüm
Birincisi, y’yi 2x – 3y ≥ 6 doğrusunun öznesi yapmaktır.
Denklemin her iki tarafından 2x çıkarın.
2x – 2x – 3y ≥ 6 – 2x
-3y ≥ 6 – 2x
Her iki tarafı da -3’e bölün ve işareti ters çevirin.
y ≤ 2x/3 -2
Şimdi y = 2x/3 – 2’nin grafiğini çizin ve çizginin altını gölgelendirin.
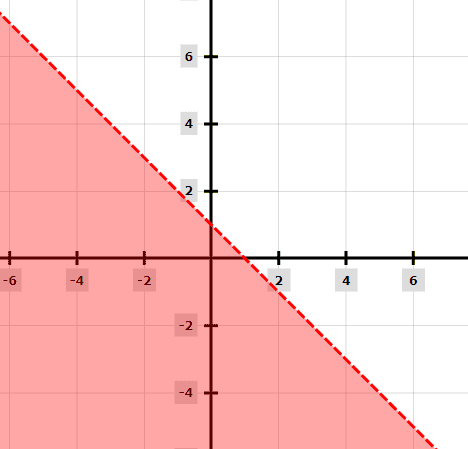
Örnek 4
x + y < 1
Çözüm
x + y = 1 denklemini y’yi formülün öznesi yapacak şekilde yeniden yazın. Eşitsizlik işareti < olduğu için grafiğimizi noktalı bir çizgi ile çizeceğiz.
Noktalı çizgiyi çizdikten sonra, < işareti nedeniyle çizginin üzerinde gölgelendirme yapıyoruz.
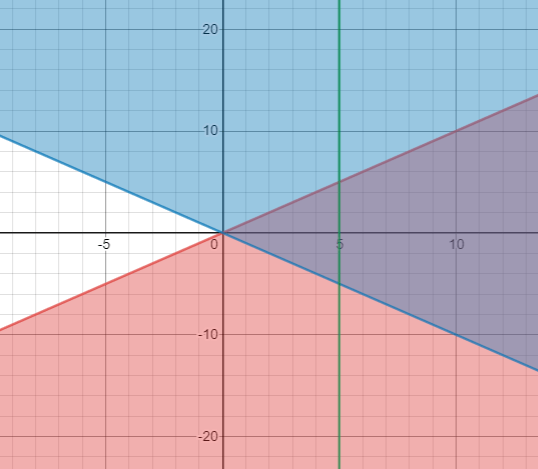
Örnek 5
Aşağıdaki eşitsizliklerin grafiksel çözümünü bulunuz:
y ≤ x
y ≥ -x
x = 5
Çözüm
Tüm eşitsizlikleri çizin.
Kırmızı, y ≤ x’i temsil eder
Mavi, y ≥ -x değerini temsil eder
Yeşil, x = 5 doğrusunu temsil eder
Ortak gölgeli alan (açıkça görülebilir) bu eşitsizliklerin grafiksel çözümüdür.