Yüksek dereceli polinom denklemlerini çözmek, fen ve matematik eğitimi alan herkes için önemli bir beceridir. Ancak, bu tür denklemlerin nasıl çözüleceğini anlamak oldukça zordur.
Bu makalede, kübik denklemlerin bölme yöntemi, Faktör Teoremi ve gruplayarak çarpanlara ayırma gibi farklı yöntemler kullanılarak nasıl çözüleceği tartışılacaktır.
Ancak bu konuya girmeden önce şunları tartışalım polinom ve kübik denklemin ne olduğu.
Bir polinom, bir toplama veya çıkarma işaretinin bir sabit ve bir değişkeni ayırdığı bir veya daha fazla terimli cebirsel bir ifadedir.
Bir polinomun genel biçimi axn + bxn-1 + cxn-2 + …. + kx + l, burada her değişkene katsayı olarak eşlik eden bir sabit vardır. Farklı polinom türleri arasında; binomlar, trinomlar ve kuadrinomlar bulunur. Polinomlara örnek olarak; 3x + 1, x2 + 5xy – ax – 2ay, 6x2 + 3x + 2x + 1 vb.
Kübik denklem, üçüncü dereceden bir cebirsel denklemdir.
Kübik bir fonksiyonun genel formu şöyledir: f (x) = ax3 + bx2 + cx1 + d. Ve kübik denklem şu şekildedir: ax3 + bx2 + cx + d = 0, burada a, b ve c katsayılar ve d sabittir.
Kübik Denklemler Nasıl Çözülür?
Kübik bir denklemi çözmenin geleneksel yolu, onu ikinci dereceden bir denkleme indirgemek ve ardından ya çarpanlarına ayırarak ya da ikinci dereceden formülle çözmektir.
İkinci dereceden bir denklemde olduğu gibi iki gerçek kökkübik bir denklemin muhtemelen üç reel kökü olabilir. Ancak ikinci dereceden bir denklemin aksine, ki bu denklemin gerçek bir çözümü olmayabilir, kübik bir denklemin en az bir gerçek kökü vardır.
Diğer iki kök gerçek ya da hayali olabilir.
Size bir kübik denklem veya herhangi bir denklem verildiğinde, her zaman önce onu standart bir biçimde düzenlemeniz gerekir.
Örneğin, size şöyle bir şey verilirse, 3x2 + x – 3 = 2/x, standart forma yeniden düzenleyecek ve şöyle yazacaksınız, 3x3 + x2 – 3x – 2 = 0. O zaman bunu herhangi bir uygun yöntemle çözebilirsiniz.
Daha iyi anlamak için aşağıda birkaç örnek görelim:
Örnek 1
2x kübik denkleminin köklerini belirleyin3 + 3x2 – 11x – 6 = 0
Çözüm
d = 6 olduğuna göre, olası çarpanlar 1, 2, 3 ve 6’dır.
Şimdi deneme yanılma yoluyla olası değerleri kontrol etmek için Faktör Teoremini uygulayın.
f (1) = 2 + 3 – 11 – 6 ≠ 0
f (-1) = -2 + 3 + 11 – 6 ≠ 0
f (2) = 16 + 12 – 22 – 6 = 0
Dolayısıyla, x = 2 birinci köktür.
Denklemin diğer köklerini sentetik bölme yöntemini kullanarak elde edebiliriz.
= (x – 2) (ax2 + bx + c)
= (x – 2) (2x2 + bx + 3)
= (x – 2) (2x2 + 7x + 3)
= (x – 2) (2x + 1) (x +3)
Dolayısıyla çözümler x = 2, x = -1/2 ve x = -3’tür.
Örnek 2
Kübik denklemin köklerini bulun x3 – 6x2 + 11x – 6 = 0
Çözüm
x3 – 6x2 + 11x – 6
(x – 1) faktörlerden biridir.
x’i bölerek3 – 6x2 + 11x – 6 ile (x – 1),
⟹ (x – 1) (x2 – 5x + 6) = 0
⟹ (x – 1) (x – 2) (x – 3) = 0
Bu kübik denklemin çözümleri x = 1, x = 2 ve x = 3’tür.
Örnek 3
x’i çözün3 – 2x2 – x + 2
Çözüm
Denklemin çarpanlarına ayırın.
x3 – 2x2 – x + 2 = x2(x – 2) – (x – 2)
= (x2 – 1) (x – 2)
= (x + 1) (x – 1) (x – 2)
x = 1, -1 ve 2.
Örnek 4
Kübik denklem x’i çözün3 – 23x2 + 142x – 120
Çözüm
Önce polinomu çarpanlarına ayırın.
x3 – 23x2 + 142x – 120 = (x – 1) (x2 – 22x + 120)
Ama x2 – 22x + 120 = x2 – 12x – 10x + 120
= x (x – 12) – 10(x – 12)
= (x – 12) (x – 10)
Bu nedenle, x3 – 23x2 + 142x – 120 = (x – 1) (x – 10) (x – 12)
Her bir faktörü sıfıra eşitleyin.
x – 1= 0
x = 1
x – 10 = 10
x – 12= 0
x = 12
Denklemin kökleri x = 1, 10 ve 12’dir.
Örnek 5
Kübik denklem x’i çözün3 – 6 x2 + 11x – 6 = 0.
Çözüm
Bu problemi bölme yöntemiyle çözmek için 6 sabitinin herhangi bir çarpanını alın;
x = 2 olsun
Polinomu x-2’ye bölerek
(x2 – 4x + 3) = 0.
Şimdi ikinci dereceden denklemi çözün (x2 – x= 1 veya x = 3 elde etmek için 4x + 3) = 0
Dolayısıyla, çözümler x = 2, x= 1 ve x =3’tür.
Örnek 6
Kübik denklem x’i çözün3 – 7x2 + 4x + 12 = 0
Çözüm
f(x) = x olsun3 – 7x2 + 4x + 12
d = 12 olduğundan, olası değerler 1, 2, 3, 4, 6 ve 12’dir.
Deneme yanılma yoluyla, f (-1) = -1 – 7 – 4 + 12 = 0 olduğunu buluruz
Dolayısıyla, (x + 1) fonksiyonun bir çarpanıdır.
x3 – 7x2 + 4x + 12
= (x + 1) (x2 – 8x + 12)
= (x + 1) (x – 2) (x – 6)
Bu nedenle x = -1, 2, 6
Örnek 7
Aşağıdaki kübik denklemi çözünüz:
x3 + 3x2 + x + 3 = 0.
Çözüm
x3 + 3x2 + x + 3
= (x3 + 3x2) + (x + 3)
= x2(x + 3) + 1(x + 3)
= (x + 3) (x2 + 1)
Bu nedenle, x = -1 ,1 -3.
Örnek 8
x’i çözün3 – 6x2 + 11x – 6 = 0
Çözüm
Çarpanlara Ayırma
x3 – 6x2 + 11x – 6 = 0 ⟹ (x – 1) (x – 2) (x – 3) = 0
Her bir faktörün sıfıra eşitlenmesi şunu verir;
x = 1, x = 2 ve x = 3
Örnek 9
x’i çözün 3 – 4x2 – 9x + 36 = 0
Çözüm
Her iki terim kümesini çarpanlarına ayırın.
x2(x – 4) – 9(x – 4) = 0
Ortak çarpanı (x – 4) çıkarmak için
(x2 – 9) (x – 4) = 0
Şimdi iki karenin farkını çarpanlarına ayırın
(x + 3) (x – 3) (x – 4) = 0
Her bir faktörü sıfıra eşitleyerek şunu elde ederiz;
x = -3, 3 veya 4
Örnek 10
3x denklemini çözün3 -16x2 + 23x – 6 = 0
Çözüm
3x bölme3 -16x2 3x elde etmek için x -2 ile + 23x – 62 – 1x – 9x + 3
= x (3x – 1) – 3(3x – 1)
= (x – 3) (3x – 1)
Bu nedenle, 3x3 -16x2 + 23x – 6 = (x – 2) (x – 3) (3x – 1)
Elde etmek için her bir faktörü sıfıra eşitleyin,
x = 2, 3 ve 1/3
Örnek 11
3x’in köklerini bulun3 – 3x2 – 90x=0
Çözüm
3 katını hesapla
3x3 – 3x2 – 90x ⟹3x (x2 – x – 30)
Çarpımı -30 ve toplamı -1 olan bir çarpan çifti bulun.
⟹- 6 * 5 =-30
⟹ -6 + 5 = -1
“bx” terimini seçilen faktörlerle değiştirerek denklemi yeniden yazınız.
⟹ 3x [(x2 – 6x) + (5x – 30)]
Denklemi çarpanlarına ayırın;
⟹ 3x [(x (x – 6) + 5(x – 6)]
= 3x (x – 6) (x + 5)
Her bir faktörü sıfıra eşitleyerek şunu elde ederiz;
x = 0, 6, -5
Kübik denklemlerin grafiksel yöntemle çözülmesi
Kübik denklemi yukarıdaki yöntemlerden herhangi biriyle çözemiyorsanız, grafiksel olarak çözebilirsiniz. Bunun için, verilen kübik denklemin doğru bir taslağına sahip olmanız gerekir.
Grafiğinin x eksenini kestiği nokta(lar) denklemin çözümüdür. Kübik denklemlerin gerçek çözümlerinin sayısı, grafiğinin x eksenini kaç kez kestiği ile aynıdır.
Örnek 12
x’in köklerini bulun3 + 5x2 + 2x – 8 = 0 grafiksel olarak.
Çözüm
Rastgele x değerlerini yerine koyarak aşağıdaki fonksiyonun grafiğini çizin:
f (x) = x3 + 5x2 + 2x – 8
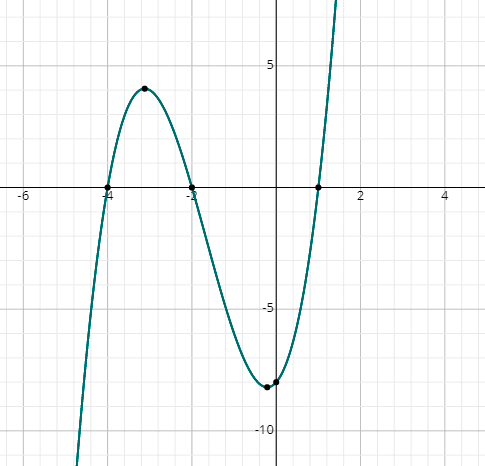
Grafiğin x eksenini 3 noktada kestiğini görebilirsiniz, bu nedenle 3 gerçek çözüm vardır.
Grafikten, çözümler şunlardır:
x = 1, x = -2 & x = -4.
